Making sense of Functors in Scala

In this blog post we will visit functors in Scala and try to reason with their existential purpose and how could we best make use of them.

A Functor in functional programming is any type that implements the map or contramap functions. Depending upon which of these methods does a type implements it falls into one of the three categories of functors, namely, covariant, contravariant or invariant functor. We will understand why are they named after variances in Scala further in the post but let's first visit them one by one.

Also, please be informed that to understand what lays ahead you must already have a good enough understanding of Type Class pattern and Higher-Kinded Types in Scala for I am not going to visit them in this post for the sake for brevity.

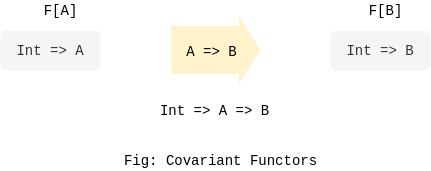
Covariant Functors

Covariant functors are also referred simply as Functor.

Formally, any type F[A] that implements a map function which given a transformation of type A => B returns type F[B].

If you aren't already aware, F[A] is a type constructor. Here it represents a generic type F parameterized by a generic type A. An example concrete implementation would be List[Int]. Applying a transformation of type say Int => String to the map function of type List[Int] would return type List[String]. And as you might already have guessed by now, List[A] is indeed a functor. Functors, however, aren't limited to simple types only. Any user defined parameterized type that implements a map function is also a Functor.

Another example of Functors worth mentioning here are single argument Scala Functions. Function definitions as we know takes at least two type parameters, one to represent the single parameter type and the other to represent return type.

However, the functor map function takes a transformation from a single type to another type. To coerce Function to the shape of a functor we have to fix any one of the type parameters. But which type parameter to fix? Let's fix the parameter type and keep the return type varying and try to implement a map function for a Scala Function to see what would it mean to map over it. We can fix the parameter type by creating a Scala type, like so, type MyFunc[T] = Function[Int, T]. Note that in practice this achieved automatically by the Scala compiler via partial unification.

Note: This requirement to fix any of the type parameters is, however, not extended to the container types like List, Option, Either, Future, etc. Containers need not be coerce to the shape of functors because they represent only single type parameter i.e., the type of the encapsulating elements. For example, Option[String].

Function is part of Scala standard library, so we won't be able to implement map function for them directly, but we could use Scala type class pattern to add map to Function. This is called as ad-hoc polymorphism.

In our example, Functor[F[_]] is Higher-Kinded Type that implements the type class which intends to add map function for any parameterized type not just Scala Function. However, functionFunctor is the type class instance implementation that knows how to map over a given function.

Now, given a function func1 of type String that we wish to map over and the transformation operation func2 of type String => Double, we could derive a function func3 of type Double like so:

Remember that func3 is a functor of type MyFunc[Double] that was fixated on parameter type Int. In order to evaluate func3 we have to invoke it explicitly by passing an argument of type Int.

It is worth mentioning here that we didn't really need to implement the Functor type class and it's type class instance. Scala's Cats library provides these implementation to us out-of-the-box.

What if we were to fix return type and keep the parameter type varying? If we would have fixed the return type instead, we would not be able to chain functions one after the other. Fixing the parameter type and keeping the return type varying is what allows us to compose functions in "appending" order. The idea simply is that if we have a function of type say Int => A and a transformation of type A => B, composing them in appending order would give us a function of type Int => B.

Functor Laws

The map function of a functor has this unique virtue of leaving the structure of the context unchanged. For example, when applied to a List, map leaves the order and the count of the list elements. This property of map makes it possible to sequence multiple computations.

This allows us to think of map not only as an iteration or transformation pattern but also as a way of sequencing computations. However, a functor has to guarantee the same semantics, whether we sequence many small operations one by one, or combine them into a larger function before mapping. To ensure this the following laws must hold true at all times:

1. Identity: States that calling a map with an identity function leaves the functor as is.

   
   

2. Composition: States that mapping function composition g o f is same as mapping f and then g.

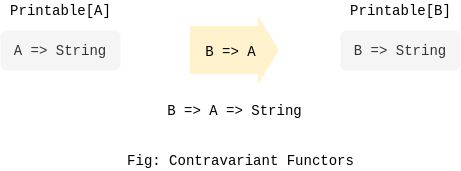
Contravariant Functors

A contravariant functor of type F[A] implements a contramap function which given a transformation of type B => A returns type F[B]. Observe that the types in transformation operation are reversed for contravariant functors.

But given a transformation of type B => A, doesn't it seems counter intuitive to be able to transform F[A] to F[B]? Let's explore this a bit further.

When it comes to contravariant functors, the transformation operation could only be applied to the types that implement functions that are fixated on the return type and keep the parameter type varying. One of such examples is Printable[A] type:

Now since this time it is the parameter type that is variable, it would only make sense to accept transformation operations that are reversed in types. This allows us to address a simple use case: given a functor of type A => String and a transformation of type B => A, we could derive a functor of type B => String by composing them in "prepending" order.

Contrived Example
If we had a Box[A] type:

We could either write a Printable for type Box[A], like so:

or given a transformation of type Box[A] => A derive the same using contramap function on any Printable of type A:

Now if we have Box[String] with Printable[String] in scope, we could print a box, like so:

Note that the contramap method only makes sense for data types that represent transformations. For example, we can't define contramap for an Option because there is no way of feeding a value in an Option[B] backwards through a function A => B.

Invariant Functors

Invariant functors implement a method called imap that is informally equivalent to a combination of map and contramap.

Contrived Example
If we had a Codec[T] type:

we could implement imap for Codec[T] like so:

This would allow us to convert, for example, Codec[String] to Codec[Int] like so:

In other words, for a type F[A] that implements functions that alternatively fixate parameter or return type, for example encode and decode functions in the example above; if we need to be able to convert F[A] to a type F[B], it would require us to implement imap function instead of map or contramap alone.

What if we have types that are varying both in parameter as well as return type?
One such example is a Monoid type:

Since both the methods empty and combine in a Monoid are varying in both parameter as well as return type, we have to provide transformations both from A => B and B => A to be able to convert a F[A] to F[B]. This also means that we could as well convert F[B] to F[A] with the same set of transformations. This however is possible to all invariant functors not just Monoids.

Given a Monoid[String], we can derive a Monoid[Symbol]:

We can reverse the derivation from Monoid[Symbol] to Monoid[String] with the same set of transformations:

Why are functors named after Scala variances?

I have explored variances in Scala at length in this post, if you wish to check it out.

Given a transformation of type A => B and a functor of type F[A], the only reason we are able to convert the functor to type F[B] is because we are able to substitute functions implemenations in F[A] covariantly i.e., we are able to replace their "return type" from A to B. Here, the conversion of type A => B is viewed as subtyping. This is where covariant functors derive their name from.

Similarly, given a transformation of type B => A and a functor of type F[A], the only reason we are able to convert the functor to type F[B] is because we are able to substitute functions implementations in F[A] contravariantly (Read more about function substitutions in the post mentioned earlier) i.e., we are able to replace their "parameter type" from B to A. This is where contravariant functors derive their name from.

Finally, invariant functors capture the case where we can convert from F[A] to F[B] via a transformation of type A => B and vice versa via a transformation of type B => A.

That's all, guys! I believe we have covered most of the aspects of functors by now and hope that functors aren't as intimidating as they seemed earlier. All the examples are available here to try.