So, you’ve come across Bloom filters and understand that, despite their probabilistic nature, they are a great fit for your use case. You’ve decided to integrate them into your system design, but you’re unsure about the optimal size and the number of hash functions needed for your specific requirements.
In this blog post, I’ll help you address these questions by not only providing guidance on how to determine the ideal parameters but also explaining the underlying mathematics that drives these decisions.
But first a quick detour!
We know that Bloom filters are p11c data structures i.e., they trade off a small chance of inaccuracies (false positives) for significant gains in memory efficiency and speed. However, we can minimize the chances of false positives by:
1. increasing the size of the Bloom filter (m in bits)
2. optimizing the number of hash functions used (k) without incurring excessive computational overhead
We also know that Bloom filters are fixed in size. As we will explore later, this fixed size means that the number of elements (n) we intend to store in the Bloom filter directly influences the probability of false positives as well.
But first let's see if can be define probability of false positives in terms the size of the Bloom filter (m in bits), the number of hash functions (k), and the number of elements (n) that we intend to store in the Bloom filter.
Probability of false positives
For a fixed bit, the probability of that bit being set to 1 by a single hash function is:
\( 1/m \)
and the probability of that bit still being 0 is:
\( (1-1/m) \)
The probability of that bit still being 0 after applying k distinct hash functions to the same element is:
\( (1-1/m)^k \)
After inserting n elements using k distinct hash functions, the probability of that bit still being 0 is:
\( (1-1/m)^{kn} \)
Conversely, the probability of that bit being set to 1 after inserting n elements using k distinct hash functions is:
\( p = 1 - (1-1/m)^{kn} \)
Since a false positive requires k random bits to be set to 1, the probability of a false positive after inserting n elements using k distinct hash functions is:
\( p = ( 1 - (1-1/m)^{kn} )^{k} \)
By now, we can either plug in the values of m, k, and n into the formula to calculate the exact value of p, or we can use calculus to derive an approximate value for p by simplifying the mathematical expressions as follows.
Rewriting the equation as:
\( p = (1 - (1-1/m)^{-m * -kn/m} )^{k} \)
and using the limit definition of e:
\( e = \lim\limits_{x \to \infty} (1-\frac{1}{x})^{-x} \)
we can approximate the probability of false positive as:
\( p \approx (1 - e^{-kn/m} )^{k} \)
We also know from the relationship between exponentials and logarithms that:
\( a^b = e^{bln(a)} \)
Hence, we can rewrite the probability of false positive approximation in its exponential form as:
\( p \approx e^{kln(1 - e^{-kn/m} )} \)
Looking at the general form of an exponential plot, it is apparent that to achieve the smallest possible value for the probability of false positive approximation, we need to minimize the exponent in the expression i.e.,
\( y = kln(1 - e^{-kn/m}) \) or,
\( y = kln(1 - e^{-k/(m/n)}) \)
The ratio m/n is a critical design parameter here, representing the bits of storage allocated per element. A higher m/n ratio generally leads to lower false positive rates, as more space is available to minimize collisions. In other words, no matter the size of the Bloom filter, you cannot keep inserting elements indefinitely, as doing so would eventually lead to an unacceptable false positive rate due to the increasing number of collisions.
Finding optimal value for k
In the equation above, if we fix the value for the ratio m/n (i.e., the values for m and n are known), we can determine the optimal number of hash functions (k) that minimizes the false positive probability for that specific ratio.
Using calculus, we can mimize of the probability of false positives by finding the local minima for
\( y = kln(1 - e^{-kn/m}) \),
such that:
\( \frac{\mathrm d}{\mathrm d k} (y) = 0 \) or,
\( \frac{\mathrm d}{\mathrm d k} (kln(1 - e^{-kn/m})) = 0 \)
Using the product rule of differentiation, we can rewrite this as:
\( ln(1 - e^{-kn/m}) \frac{\mathrm d}{\mathrm d k} (k) + k\frac{\mathrm d}{\mathrm d k} (ln(1 - e^{-kn/m})) = 0 \)
Since \(\frac{\mathrm d}{\mathrm d x} (x) = 1 \), rewriting the above equation as:
\( ln(1 - e^{-kn/m}) + k\frac{\mathrm d}{\mathrm d k} (ln(1 - e^{-kn/m})) = 0 \)
Let’s refer to this equation (a + b = 0) as equation 1, which we will solve in parts and revisit later.
Using the chain rule of differentiation, we can rewrite b as:
\( k\frac{\mathrm d}{\mathrm d (1 - e^{-kn/m})} (ln(1 - e^{-kn/m})) \frac{\mathrm d}{\mathrm d k} (1 - e^{-kn/m}) \)
Since for x > 0, \( \frac{\mathrm d}{\mathrm d x} (ln(x)) = \frac{1}{x} \), we can rewrite b as:
\( \frac{k}{(1 - e^{-kn/m})} \frac{\mathrm d}{\mathrm d k} (1 - e^{-kn/m}) \)
Using the difference rule of differentiation, we can rewrite b as:
\( \frac{k}{(1 - e^{-kn/m})} (\frac{\mathrm d}{\mathrm d k} (1) - \frac{\mathrm d}{\mathrm d k} (e^{-kn/m})) \)
Since \(\frac{\mathrm d}{\mathrm d x} (CONSTANT) = 0 \), rewriting the above expression as:
\( \frac{k}{(1 - e^{-kn/m})} (0 - \frac{\mathrm d}{\mathrm d k} (e^{-kn/m})) \) or,
\( - \frac{k}{(1 - e^{-kn/m})} \frac{\mathrm d}{\mathrm d k} (e^{-kn/m}) \)
Using the chain rule of differentiation, we can rewrite the expression as:
\( - \frac{k}{(1 - e^{-kn/m})} \frac{\mathrm d}{\mathrm d (-kn/m)} (e^{-kn/m}) \frac{\mathrm d}{\mathrm d k} (-kn/m) \)
Since \( \frac{\mathrm d}{\mathrm d x} (e^x) = e^x \), rewriting the expression as:
\( - \frac{ke^{-kn/m}}{(1 - e^{-kn/m})} \frac{\mathrm d}{\mathrm d k} (-kn/m) \)
Since \( \frac{\mathrm d}{\mathrm d k} ak = a\frac{\mathrm d}{\mathrm d k} k = a\), rewriting the expression as:
\( - \frac{ke^{-kn/m}}{(1 - e^{-kn/m})} (-n/m) \) or,
\( \frac{(kn/m)e^{-kn/m}}{(1 - e^{-kn/m})} \)
Now we can revisit and rewrite the equation 1 as:
\( ln(1 - e^{-kn/m}) + \frac{(kn/m)e^{-kn/m}}{(1 - e^{-kn/m})} = 0 \) or,
\( \frac{(kn/m)e^{-kn/m}}{(1 - e^{-kn/m})} = - ln(1 - e^{-kn/m}) \)
Taking exponentials on both sides, we get
\( e^{ \frac{(kn/m)e^{-kn/m}}{(1 - e^{-kn/m})} } = e^{ - ln(1 - e^{-kn/m}) } \)
As we already know from the relationship between exponentials and logarithms that:
\( a^b = e^{bln(a)} \)
Using this property, we can rewrite the above equation as:
\( e^{ \frac{(kn/m)e^{-kn/m}}{(1 - e^{-kn/m})} } = ( 1 - e^{-kn/m} )^{-1} \)
Assuming \( x = e^{ (-kn/m) } \), we can rewrite the equation as:
\( e^{ \frac{(kn/m)x}{(1 - x)} } = ( 1 - x )^{-1} \) or,
\( e^{ -(kn/m)(\frac{-x}{(1 - x)}) } = ( 1 - x )^{-1} \) or,
\( x^{ -\frac{x}{(1 - x)} } = ( 1 - x )^{-1} \) or,
\( x^{ \frac{x}{(1 - x)} } = ( 1 - x ) \)
Taking logarithm both the sides, we can rewrite the equation as:
\( ln(x^{ \frac{x}{(1 - x)} }) = ln( 1 - x ) \)
Using power rule of logarithm, we can rewrite the equation as:
\( \frac{x}{(1 - x)} ln(x) = ln( 1 - x ) \) or,
\( xln(x) = (1-x)ln( 1 - x ) \)
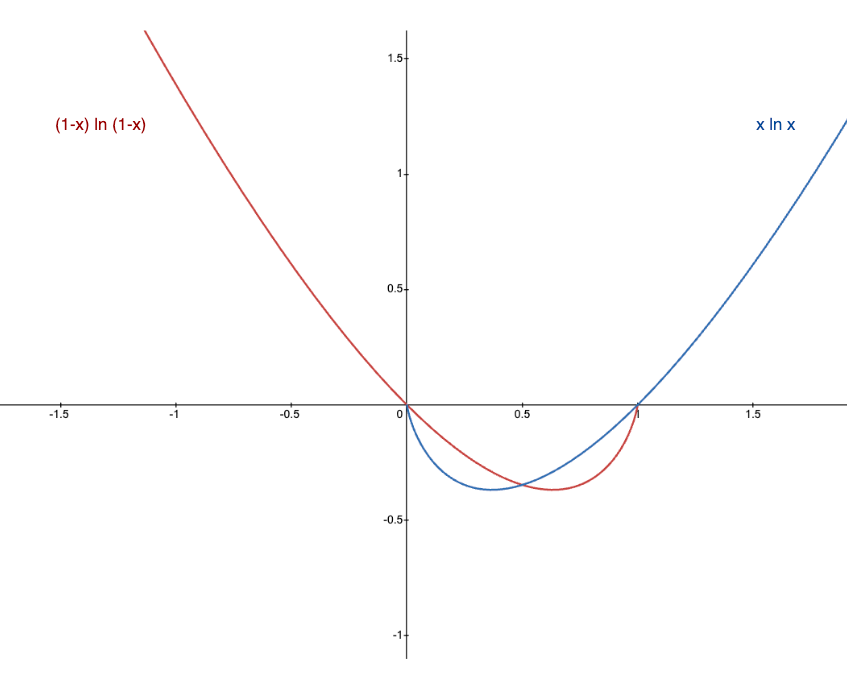
Looking at the plot for above expressions on both sides, we can observe that for non-zero LHS and RHS, LHS = RHS when x = 0.5 i.e., when
\( e^{ -kn/m } = 0.5 \) or,
\( (-kn/m) ln (e) = ln (1/2) \)
Since ln (e) = 1, rewriting the equation as:
\( (-kn/m) = ln (1/2) \) or,
\( (-kn/m) = ln (2^{-1}) \)
Using power rule of logarithm, rewriting the equation as:
\( (-kn/m) = -ln (2) \) or,
\( (kn/m) = ln (2) \)
And thus, we have k defined in terms of the ratio m/n, which represents the bits of storage allocated per element, like so:
\( k = (m/n) ln (2) \)
Finding optimal value for m
Going back to our definition of the probability of false positives:
\( p \approx e^{kln(1 - e^{-kn/m} )} \)
and substituting our newly found value of \( k = (m/n) ln (2) \), we get:
\( p \approx e^{(m/n)ln(2)ln(1 - e^{-(m/n)ln(2)(n/m)} )} \) or,
\( p \approx e^{(m/n)ln(2)ln(1 - e^{-ln(2)} )} \) or,
\( p \approx e^{(m/n)ln(2)ln(1 - \frac{1}{e^{ln(2)}} )} \)
From the relationship between exponentials and logarithms we know that:
\( a^b = e^{bln(a)} \)
Using this property, we can rewrite the above equation as:
\( p \approx e^{(m/n)ln(2)ln(1 - 1/2 )} \) or,
\( p \approx e^{(m/n)ln(2)ln(1/2 )} \) or,
\( p \approx e^{(m/n)ln(2)ln( 2 ^ { -1 } ) } \) or,
\( p \approx e^{-(m/n)ln(2)ln(2) } \)
Taking logarithm on both sides, we get:
\( ln(p) \approx -(m/n) ln(2) ln(2) \) or,
\( m/n \approx -\frac{ln(p)}{ ln(2) ln(2) } \) or,
\( m/n \approx -\frac{1}{ ln(2) } (\frac{ln(p)}{ ln(2) }) \)
Using change of base rule of logarithms, we can rewrite the equation as:
\( m/n \approx -\frac{1}{ ln(2) } log(p) \)
Substituting the approximate value of \( \frac{1}{ ln(2) } \approx 1.4427 \), we can express the ratio m/n in terms of the probability of false positives p as follows:
\( m/n \approx -1.4427 log(p) \)
Now we can even express the number of hash functions k in terms of probability of false positives p as follows:
\( k \approx -log(p) \)
Putting values of k and m to test
Suppose we're okay with around a 2% false positive rate. Substituting this to values of k and m, we get:
\( m/n \approx -1.4427 log(0.02) \approx 8.1424 \)
\( k \approx -log(0.02) \approx 5.6439 \)
This means that for a 2% false positive rate, we would need approximately 5 hash functions and regardless of the size of the Bloom filter, we must ensure that the bits of storage allocated per element are never lower than 8. Remember that for a fixed-sized Bloom filter, as the number of elements inserted to Bloom filter (n) increases, the ratio m/n decreases, resulting in increased collisions and false positives.
If we were to store 10 million elements, the size of the Bloom filter (m) would be:
\( m = 8 * 10\ million = 80\ million\ bits \)
To convert this into bytes:
\( Size\ in\ bytes = \frac {80\ million\ bits}{8} = 10MB \)
Thus, to store 10 million elements, the Bloom filter would require a total size of 10MB to achieve the desired false positive rate.
That’s all for this blog. I hope it’s been insightful and serves as the only guide you’ll need to understand the detailed mathematical derivations for answering the initial questions—finding the optimal size (m) and the number of hash functions (k) for your specific requirements—thereby offering clarity on designing an efficient Bloom filter tailored to your needs.
References